Linked List Cycle II

Given the HEAD of a linked list, return the node where the cycle begins. If there is no cycle, return NULL. In the previous Linked List Cycle, we have seen how to determine a cycle in the Linked List. So if you haven't solved it yet, go ahead and solve it first, because we are going to skip explaining that part here.

Let's take Slow and Fast pointer at the HEAD and first determine whether the Linked List has a cycle or not.

Determine the Cycle

After the initialization, let's iterate through the loop to find out if the linked list has any cycle in it.

Since, both slow and fast pointer meet at the same node [7], so the given Linked List has Cycle. Let's write the code for this part

# Definition for singly-linked list.
# class ListNode:
#	def __init__(self, x):
#		self.val = x
#		self.next = None

class Solution:
	def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
		has_cycle = False
		slow, fast = head, head
		while fast and fast.next:
			slow = slow.next
			fast = fast.next.next
			if slow == fast:
				has_cycle = True
				break;
		
		if not has_cycle:
			# No cycle, return NULL
			return None
		# At this point we are sure that the linked list has a cycle,
		# Let's find out the beginning of the cycle

Find the Beginning of the Cycle

According to Floyd's Tortoise and Hare algorithm, the distance between the Meeting Point and Beginning Node of cycle is equal to the distance between the Head Node and Beginning Node of cycle.

Let's assume,
P = Distance between Head and Beginning of the Cycle
X = Distance between Meeting point and Beginning of the Cycle

Need to prove P = X to prove this algorithm mathematically.

Now Let's assume, C = Length of the Cycle.
The Key point is,

To meet with slow at node 7, the fast pointer has traveled the cycle completely 1 time and (C - X) distance.

So the total distance covered by fast pointer = P + C + C - X and
the total distance covered by slow pointer = P + C - X

Another Key point we already know is, F = 2(S)
hence, the equation is

	P + 2C - X = 2(P + C - X)
=>  P + 2C - X = 2P + 2C - 2X
=>  P - X = 2P - 2X
=>  P - X = 0
=>  P = X [PROVED]

Since the distance P = X, let's take another pointer curr from HEAD and move the slow and curr at the same speed (1 node at a time). The Node where both the slow and curr pointer meet is the Beginning of the Cycle

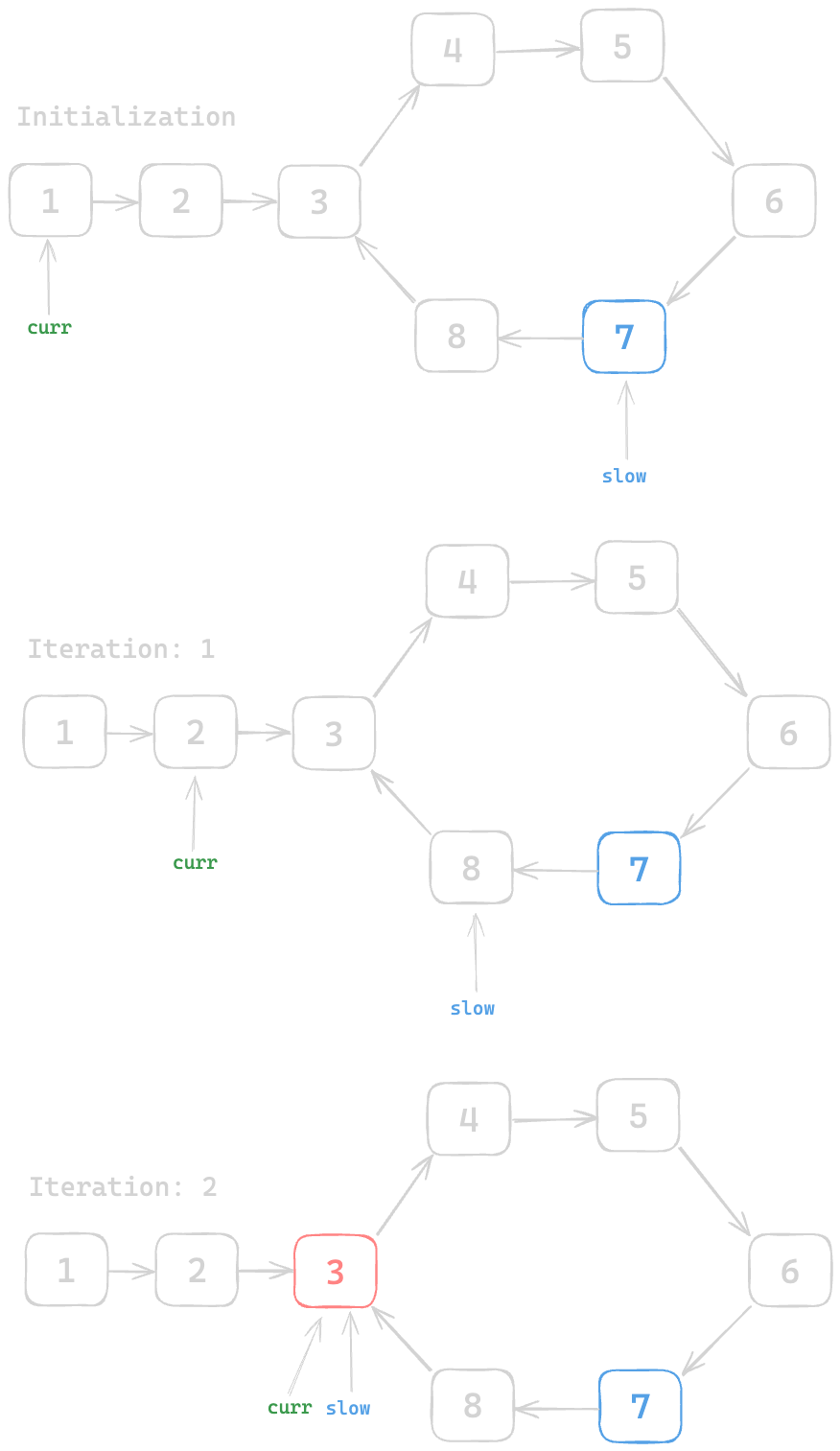
Since both slow and curr pointer meet with node 3, we have just found the beginning node of the cycle. Let's code it up

Complete Code Snippet

class Solution:
	def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
		has_cycle = False
		slow, fast = head, head
		while fast and fast.next:
			slow = slow.next
			fast = fast.next.next
			if slow == fast:
				has_cycle = True
				break;
		
		if not has_cycle:
			# No cycle, return NULL
			return None
		# At this point we are sure that the linked list has a cycle,
		# Let's find out the beginning of the cycle
		curr = head
		while curr != slow:
			curr = curr.next
			slow = slow.next
		# both slow and curr meet at a node
		# we can return any of the slow or curr pointer. 
		# but let's return the curr pointer 
		return curr

Thanks for Stopping by! Happy Leet coding.

Connect with me on