Linked List Cycle

Given the Head of a Linked List. Return true if there is a cycle in the linked list. Otherwise, return false.
If there is some node in the list that can be reached again by continuously following the next pointer, that means there is a cycle in a linked list like this example bellow.

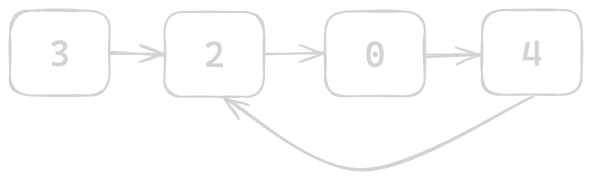
The given Linked List has a cycle, because the Tail [4] is connected to the second node [2]
Before solving this problem let's build the general intuition.

Intuition

Suppose Two friends (S and F) have gone to a Circular Park (because the rode inside the park is connected like a circle like the bellow image), where S can Walk and F can Run.

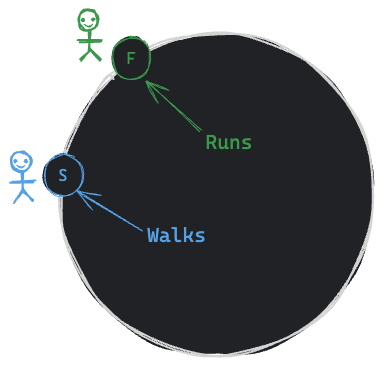
Since the rode is a connected circular path (cycle) it's guaranteed that F will cross S again, meaning S and F will meet each other at some point. Let's visualize from the bellow picture.

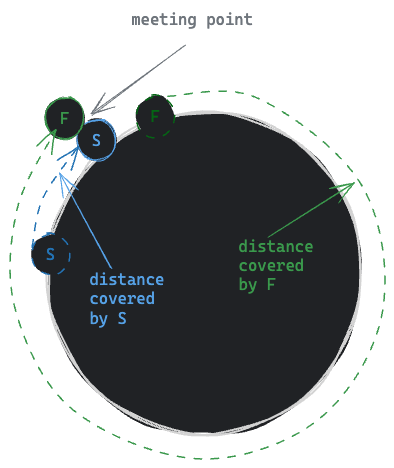
As we can see that S crossed a few distance where F cross all the way and meets with S at some point in the circular path.
Why they are meeting?

1. The path is a cycle (connected circular path)
2. F has more speed than S

🤔 If the path was not circular would they ever met?
Ans: No

🤔 If F and S has same speed, would they ever met?
Ans: No

Now we got the General Concept, Let's prove it mathematically.

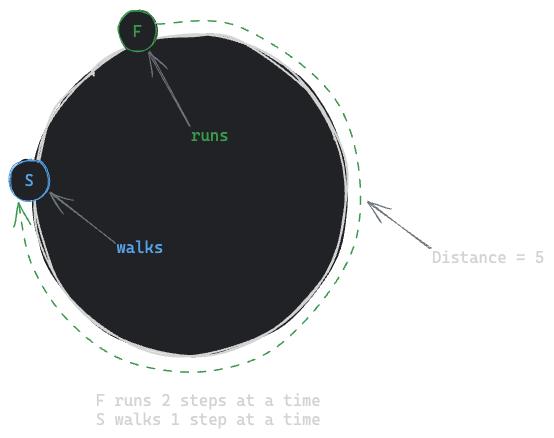
Assume the Distance between F and S is 5.
F can run 2 steps at a time where S can walk 1 step at a time.
Let Distance D = 5, Speed of F = 2 and Speed of S = 1
Let's calculate the distance after S and F moves.

1. When F moves, the distance is decreased by 2 (D - F)
2. At the same time S moves so that the distance again increased by 1 (D + S)
   Therefore, the equation is D = D - F + S
   We will keep evaluating this equation until D = 0

iteration 1:
	D = 5 - 2 + 1
	D = 4
iteration 2:
	D = 4 - 2 + 1
	D = 3
iteration 3:
	D = 3 - 2 + 1
	D = 2
iteration 4:
	D = 2 - 2 + 1
	D = 1
iteration 5:
	D = 1 - 2 + 1
	D = 0

After 5 iteration, the distance between S and F is 0, that means they will meet together after these 5 iterations. Now apply this intuition on the given Linked List.

Pointer Placement

Hope you have already noticed that we are going to use a special technique of Two Pointer algorithm named Slow Fast Pointer. We have already used Slow Fast Pointer in Middle of the Linked List. Try to solve it first, It will make more sense to understand this problem.

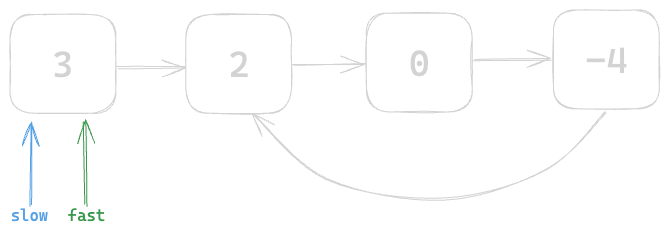
Let's place both slow and fast pointer at the Head of the Linked List and start moving them.
Fast pointer will move 2 nodes at a time while Slow pointer will move 1 node at a time. Keeping that in mind let's start iterating.

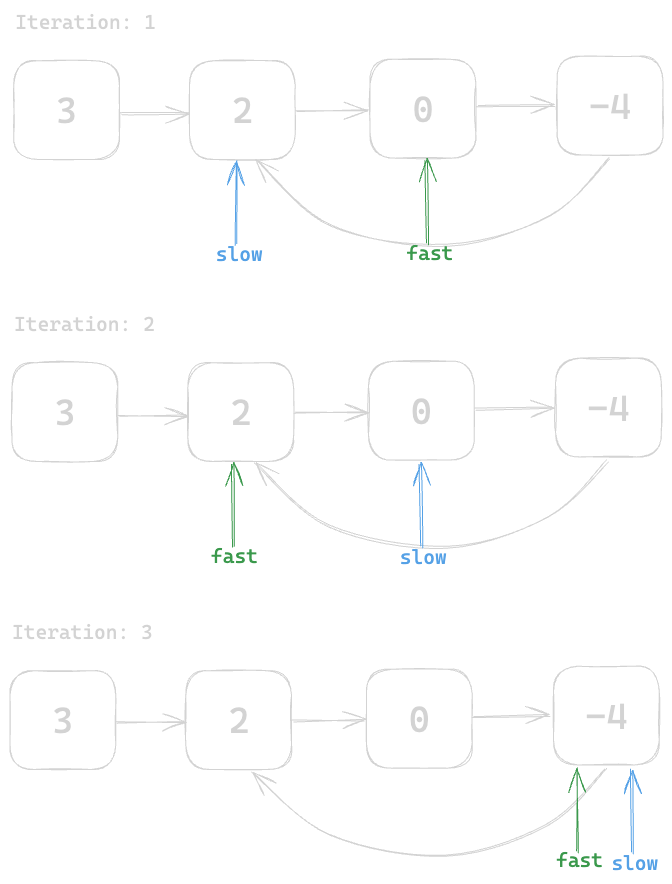
Looks like both slow and fast pointers have met at the Last Node of the Linked List, that means the Linked List has Cycle (Loop) in it. Let's implement the code

Code Snippet

# Definition for singly-linked list.
# class ListNode:
	# def __init__(self, x):
	# self.val = x
	# self.next = None

class Solution:
	def hasCycle(self, head: Optional[ListNode]) -> bool:
		# initially the slow and fast is pointing at the head
		slow, fast = head, head
		
		# need to check if fast.next is not null
		# to avoid NullPointerException for fast.next.next
		while fast and fast.next:
			slow = slow.next
			fast = fast.next.next
			
			# if the linked list contains a cycle,
			# then the fast pointer will meet with the slow pointer at a node
			# we need to check both slow and fast are pointing at the same node
			if slow == fast:
				return True
		
		# the pointers have never met with each other
		return False

Thanks for Stopping by! Happy Leet coding

Connect with me on