Find The Duplicate Number

Given an integer array nums with length n + 1, where the values can be in range [1 to n] inclusive. There must be a duplicate number in the array which needs to be find out.
The constrains are:

1. We can not modify the array.
2. We must solve this problem in O(n) Time.
3. Can not use any additional space, meaning the memory complexity must be O(1).

Intuition

In the problem description we have been told that There must be a duplicate number, but what is the guarantee? Let's assume the array length n + 1 = 5 so the last index n = 4 and the values in the array can be in range [1 to 4] which is basically [1, 2, 3, 4]. But we have 5 slots to put 4 values, so at least there will be one duplicate number

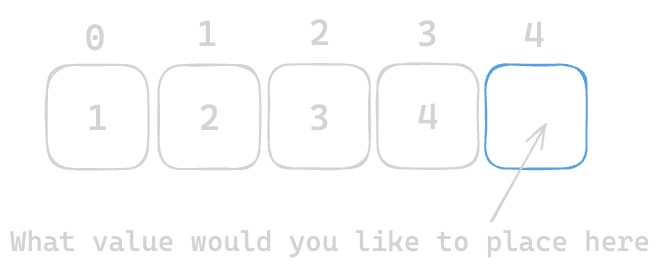
Any value you choose in range [1 to 4] would be a duplicate number. Let's select 2

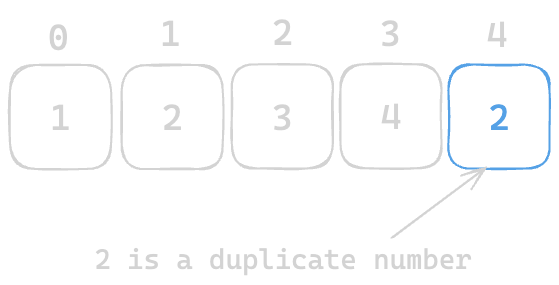
We are tasked to find out this duplicate number. Let's discuss about few approches

1. To find the duplicate number we usually user HashSet but it would cost extra O(n) space so we can not use that.
2. We could so solve it but sorting the array so the duplicate numbers would be next to each other, but we can not modify the array, so we can not sort it. Besides, if we use most efficient merge sort algorithm, it would take O(nLogn) which doesn't satisfy the condition that we must solve it O(n) time
   So what can we do? If we observe closely we can see that one values is the index of another value. For example nums = [1, 3, 4, 2, 2]. Let's take a look at the diagram.
   

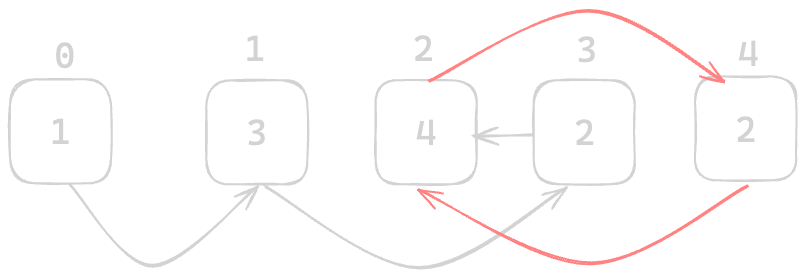
Marking Technique

If we could modify the array we could use Marking Technique to find the duplicate number. It's a very interesting technique and I can't resist myself to illustrate it.

class Solution:
	def findDuplicate(self, nums: List[int]) -> int:
		for num in nums:
			index = abs(num) - 1
			# is already negative
			if nums[index] < 0:
				# that means num has been seen previously
				# so num is a duplicate number
				return num
			else:
				nums[index] *= -1
		# no duplicate number. but code will never reach here, beacuse we already know, there must be one repeating / duplicate number.
		return -1 

Pretty interesting right? But unfortunately we can not use this method because the array is immutable, we can not modify the array.

Floyd's Tortoise and Hare

Now we have only one choice left that is Floyd's Tortoise and Hare which is a cycle detection algorithm in a Linked List, must check Linked List Cycle II for deep understanding of this algorithm, because I'm going to skip the mathematical explanation of this algorithm here.

Now the question can be, we have an Array not a Linked List, how can we even use this algorithm to solve this problem? Let's make a linked list out of the array

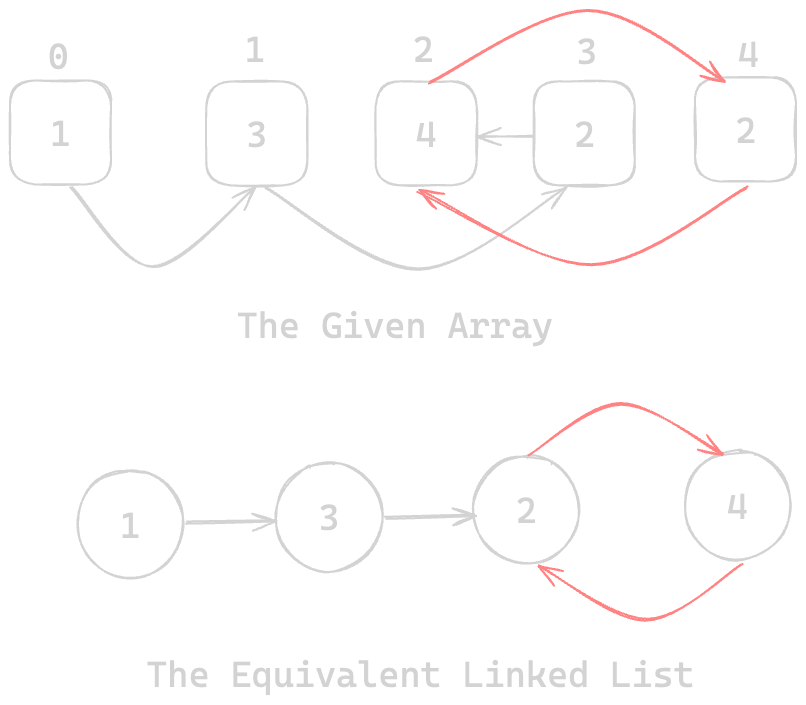
As we can see 2 -> 4 and 4 -> 2 is a cycle. If we can find out the beginning of the cycle, that would be the duplicate number. So now it's all about Linked List Cycle II

Find the intersection point

in Linked List Cycle we have seen how to detect a cycle in a Linked List, we are going to apply the same technique for our given array.
The idea is we will take slow and fast pointers. slow moved 1 step and fast jumps 2 steps at a time. If they meet that means the Linked List has a cycle. But we already sure that the array has at least one duplicate number which means there must be a cycle. We just need to find the point where both of the pointers meet.

Staring both slow and fast at index 0

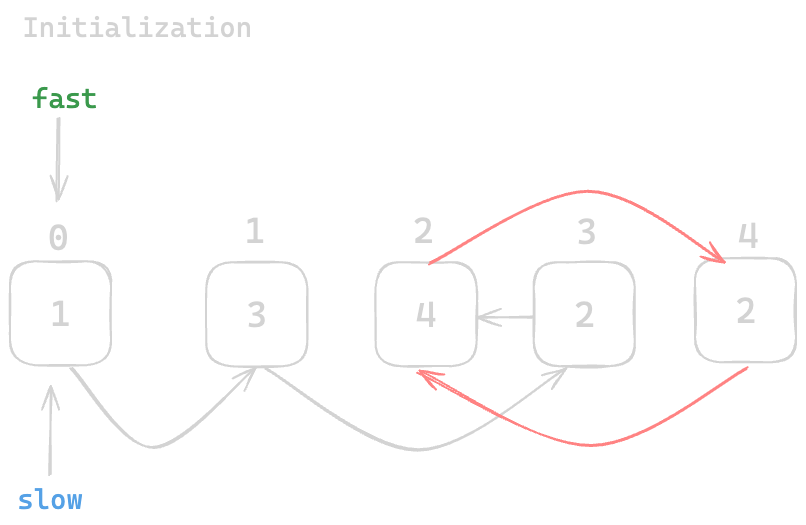
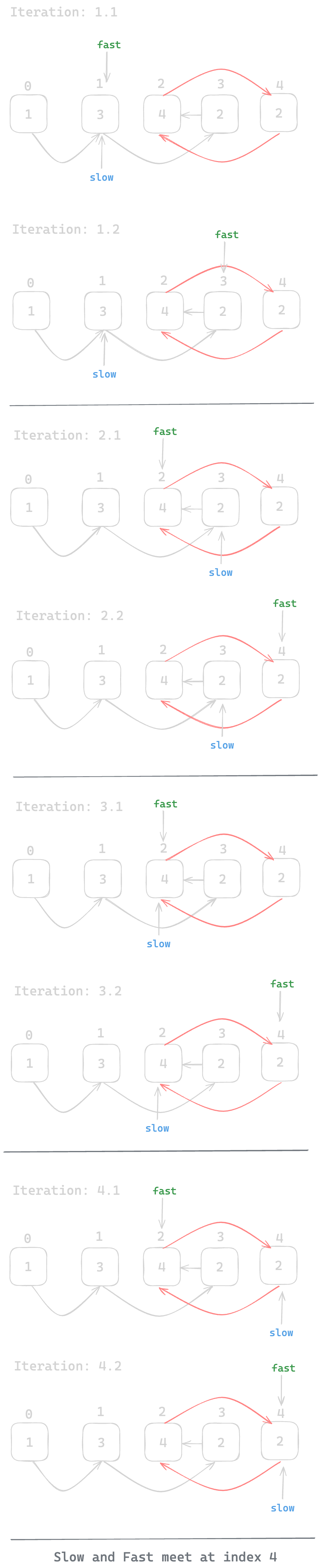
Now move slow one steps and fast two steps in each iteration. We will keep iterating until they meet with each other. Let's visualize

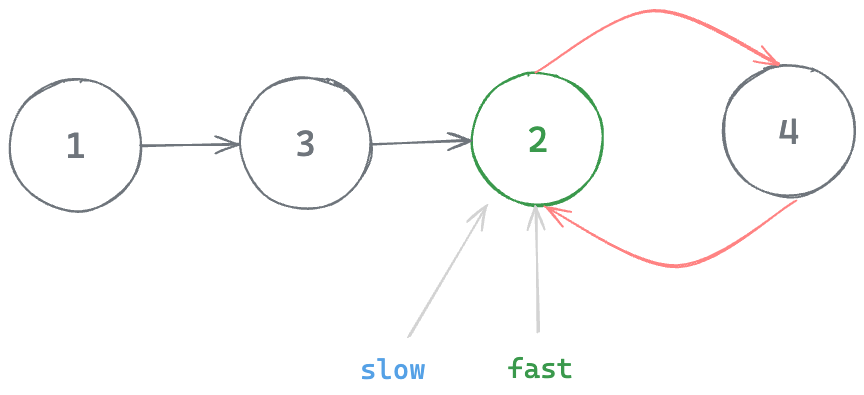
So the equivalent Linked List would look like this

Let's write the code for cycle detection

class Solution:
	def findDuplicate(self, nums: List[int]) -> int:
		slow, fast = nums[0], nums[0]
		while True:
			slow = nums[slow]  # just like slow = slow.next
			fast = nums[nums[fast]]  # just like fast = fast.next.next
			if slow == fast:
				# got the intersection point
				break

According to Floyd's algorithm The distance between beginning of the cycle and the meeting point is equal to the distance between of beginning of the cycle and the staring node of the the Linked List.
Therefore, let's take another slow2 pointer and keep slow and slow2 moving until they meet with each other. Their meeting point will be the beginning of the cycle hence the duplicate number

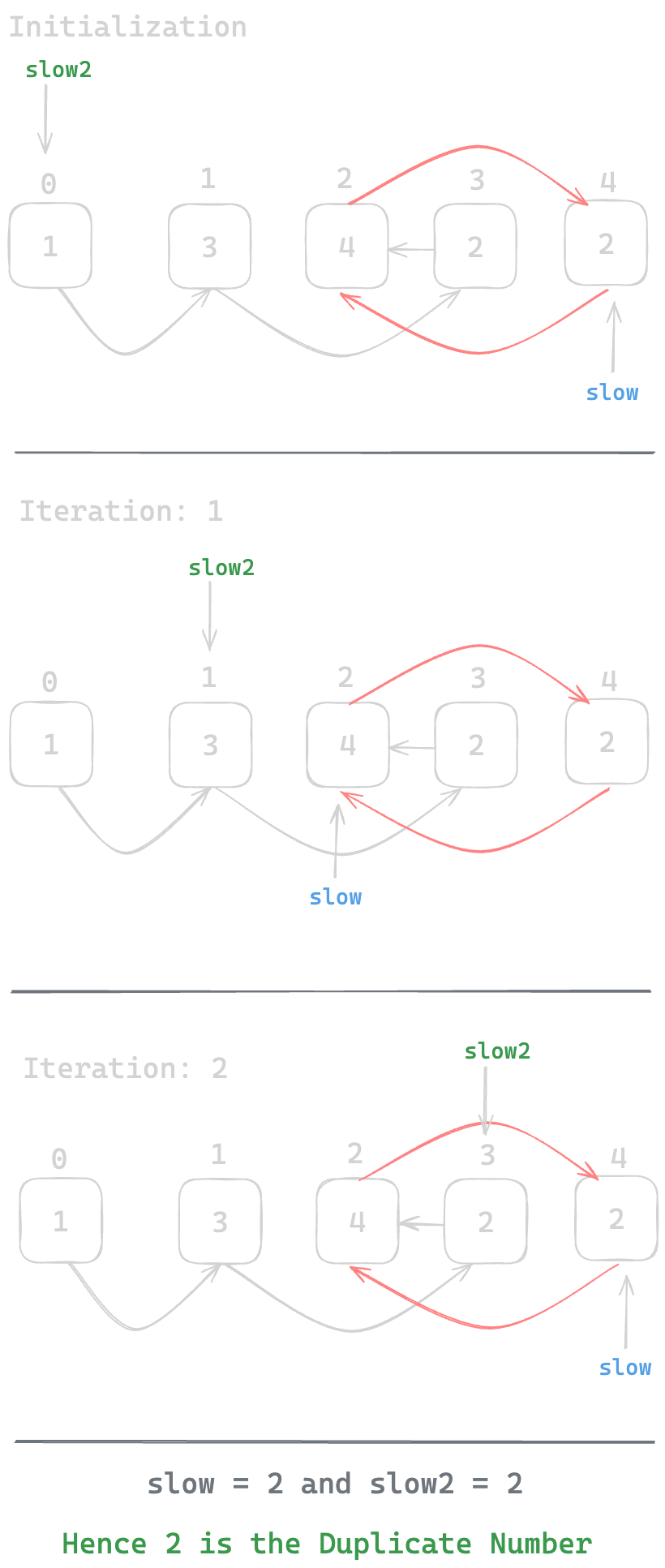
The equivalent linked list would look like this

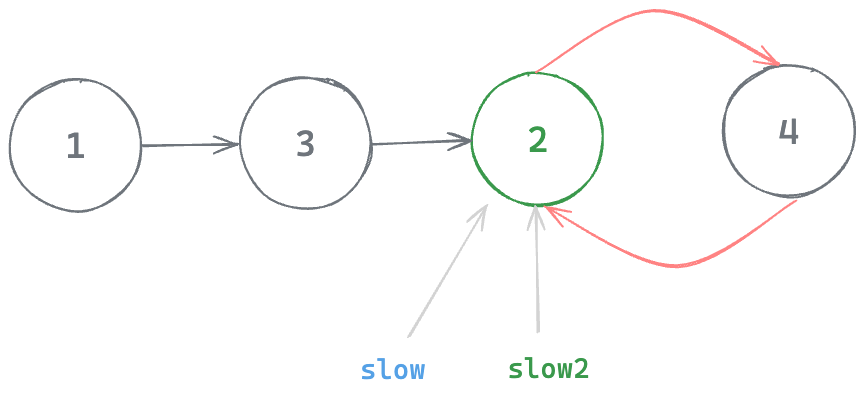
So node 2 is the beginning of the cycle in the Linked List hence 2 is the duplicate value in the Array. Let's write the complete code altogather

Complete Code Snippet

class Solution:
	def findDuplicate(self, nums: List[int]) -> int:
		slow, fast = nums[0], nums[0]
		
		# find slow fast meeting point
		while True:
			slow = nums[slow]  # just like slow = slow.next
			fast = nums[nums[fast]]  # just like fast = fast.next.next
			if slow == fast:
				# got the intersection point
				break
		
		# find the beginnig of the cycle
		slow2 = num[0]
		while slow != slow2:
			slow = nums[slow]
			slow2 = nums[slow2]
		
		# slow and slow2 has met at the beginning of the cycle hence pointing at the duplicate number
		return slow

Complexity Analysis

Time Complexity: O(n) where n is the number of nodes in the array
Memory Complexity: No extra memory user.

Thanks for Stopping by! Happy Leet coding

Connect with me on