Valid Anagram
What is Anagram
An anagram is a word or phrase formed by rearranging all the letters of another, maintaining their original frequency. For instance, cat and act are anagrams but rat and car is not anagrams.
Problem Statement
Given two strings s and t, return true if t is an anagram of s, and false otherwise.
Example 1:
Input: s = "anagram", t = "nagaram"
Output: true
Example 2:
Input: s = "rat", t = "car"
Output: false
So they are gonna give two strings s and t. Need to return if both of the strings are Anagrams or not
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
Sorting Solution
Solution that initially came into my mind is sorting. So if we sort both of the strings, the anagrams strings will be exactly equal, otherwise the given strings are not anagrams. Let's breakdown with couple examples
| Input (s) | sorted(s) | Input (t) | sorted(t) | is_anagram |
|---|---|---|---|---|
| anagram | ['a', 'a', 'a', 'g', 'm', 'n', 'r'] | nagaram | ['a', 'a', 'a', 'g', 'm', 'n', 'r'] | true |
| rat | ['a', 'r', 't'] | car | ['a', 'c', 'r'] | false |
for the first example, the sorted result is equal, that means anagram and nagaram are Anagrams. However the sorted value for rat and cat is unequal which clearly means, they are not Anagrams.
Code Snippet
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
return sorted(s) == sorted(t)
Complexity Analysis
Time Complexity:
- Sorting both strings
sandtindividually takes O(N log N) time each. - Comparing two sorted strings takes O(N) time.
- Since we perform sorting twice, the overall time complexity is:
O(NlogN) + O(NlogN) + O(N) = O(NlogN)
Since theO(N)term is negligible compared toO(N log N))
Thus, the final time complexity remains O(N log N), where N is the length of the input strings. Can we improve the time complexity? We will be exploring that shortly.
Space Complexity:
We are not using any extra space to solve the problem, so the space complexity is O(1)
More Optimal Approach
If you want a more optimal solution, you can use a hash table (dictionary) or an array of size 26 (for lowercase English letters) to count character frequencies. This approach reduce the time from O(N log N) to O(N). Let's talk about it 🚀
Hashing solution (Optimal)
This solution only works for equal length strings, and we also know if the length of the given strings are unequal, that clearly indicates not anagrams.
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
Now, we will count the frequency of each letters from both of the given strings s and t and map them into a HashMap (a.k.a dictionary in python).
Let's check with s = anagram and t = nagaram
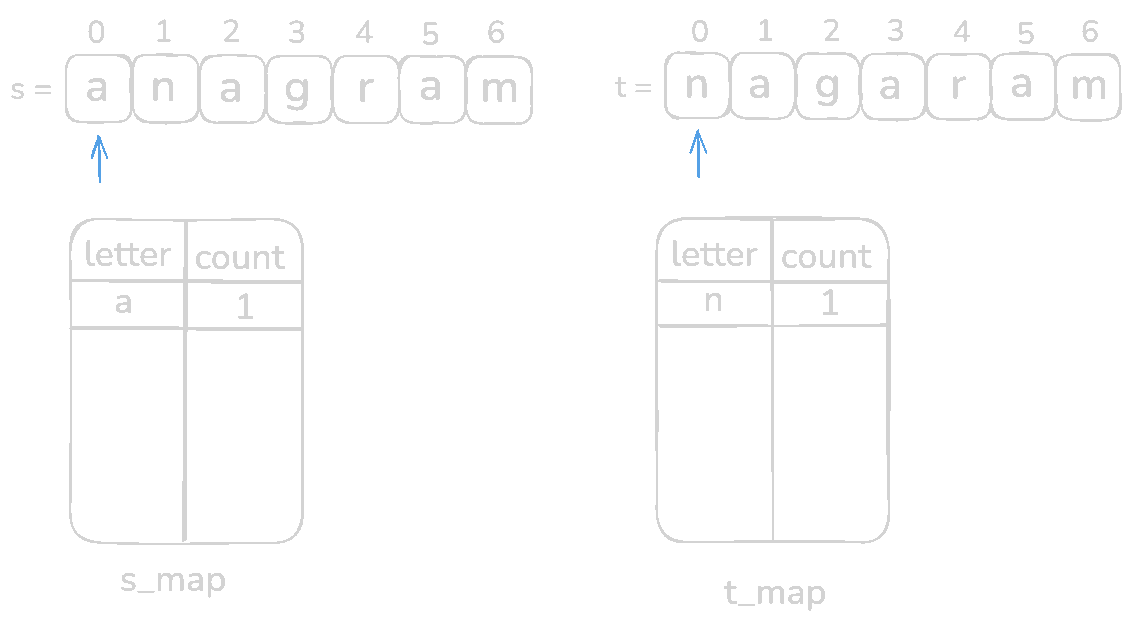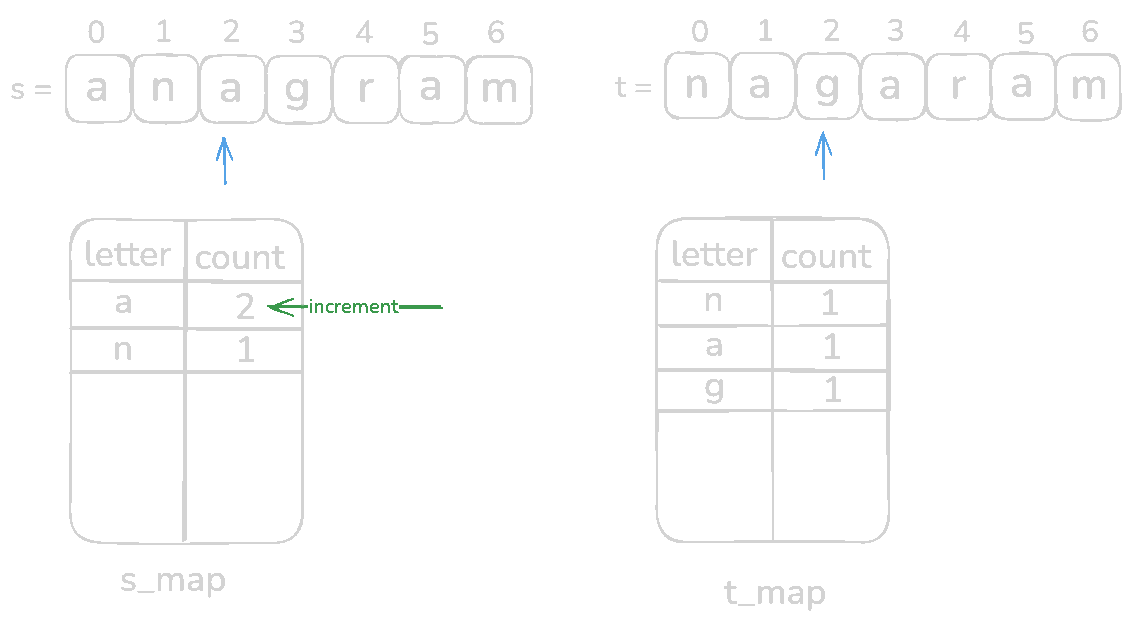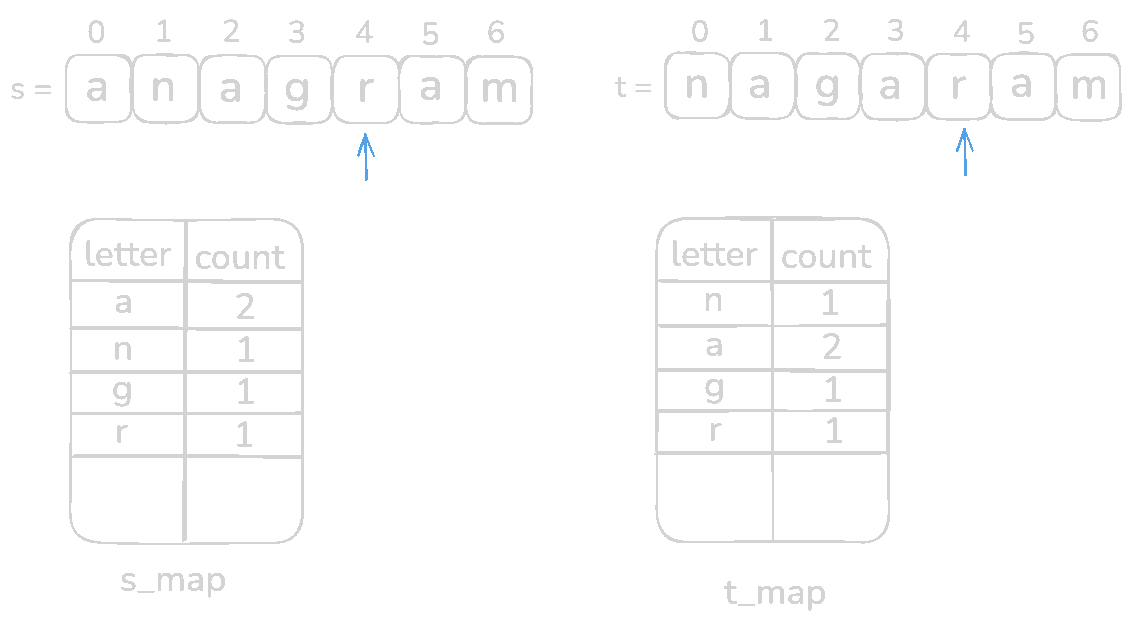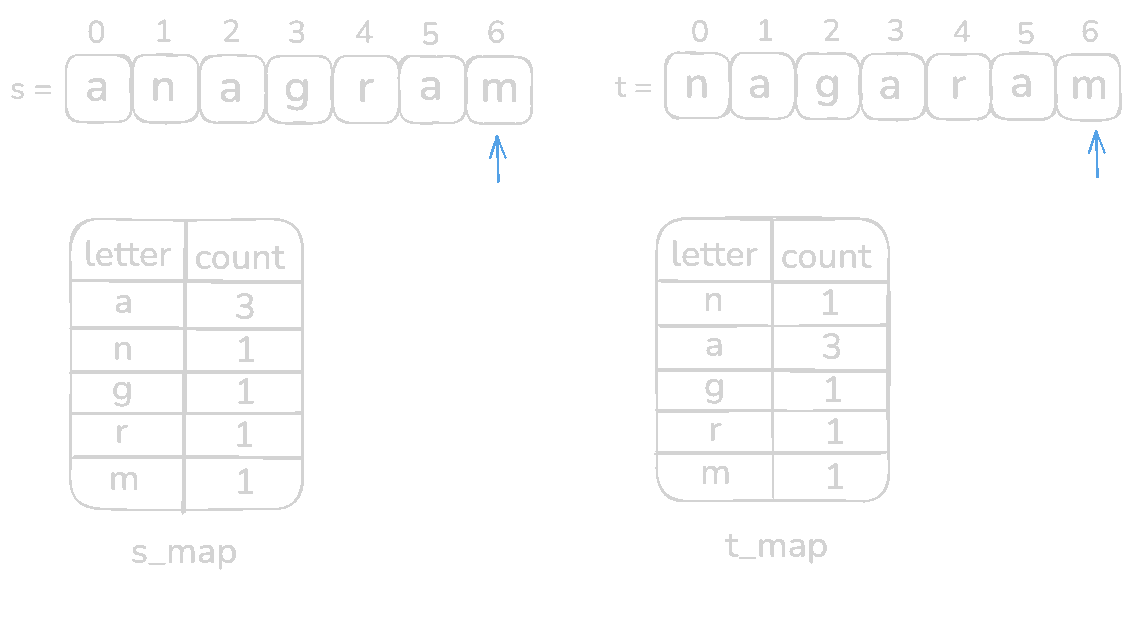
Code for this section,
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
s_map: dict[str, int] = {}
t_map: dict[str, int] = {}
for i in range(len(s)):
s_freq[s[i]] = s_freq.get(s[i], 0) + 1
t_freq[t[i]] = t_freq.get(t[i], 0) + 1
Now the final part, validation. In this step, we will check if both of the HashMaps has the exact same count for a specific letter. Let's iterate through s_map (any of the HashMaps can be used).
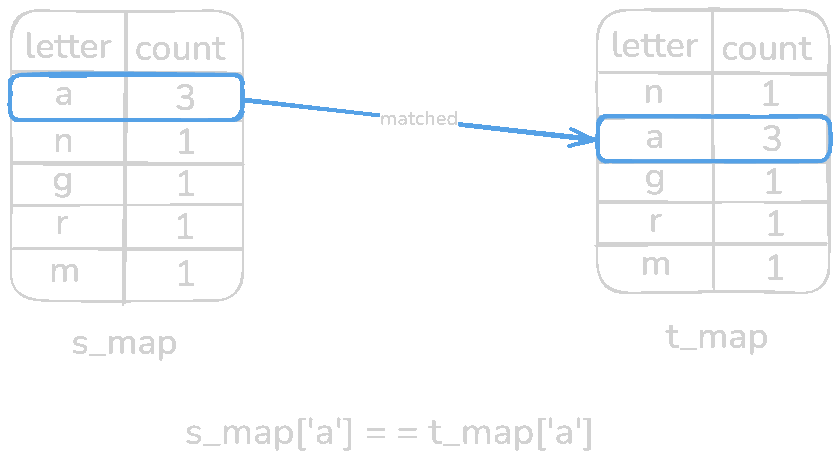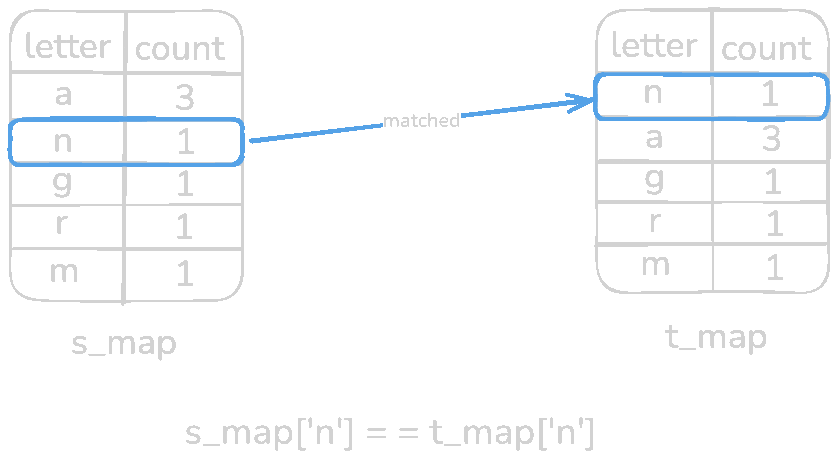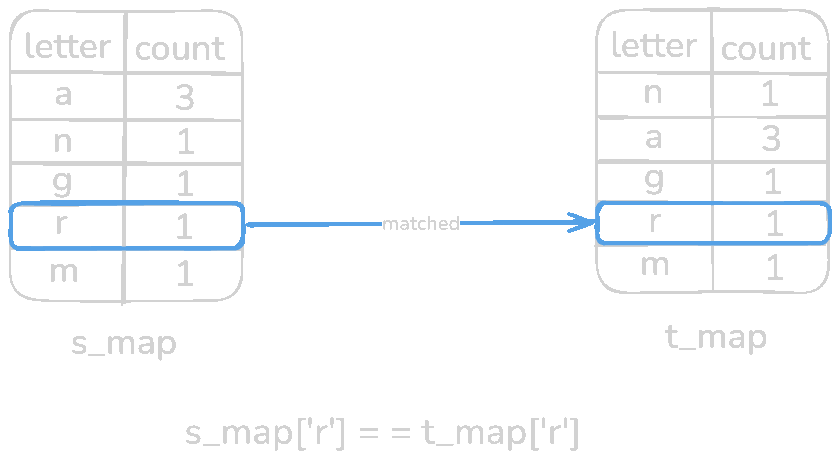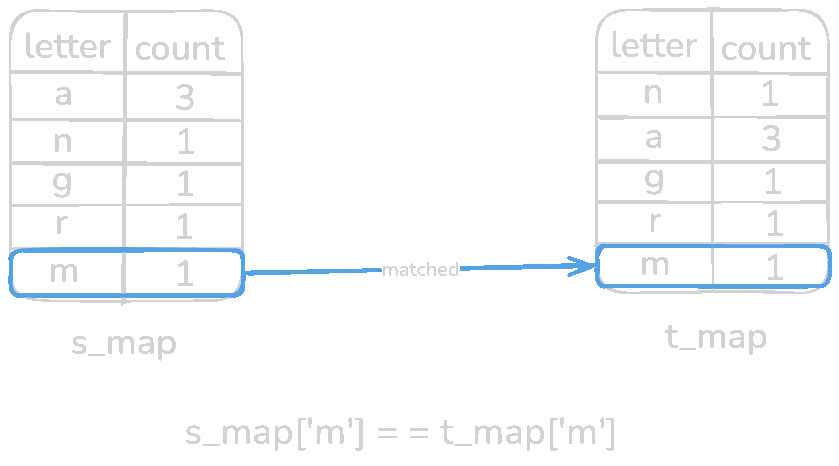
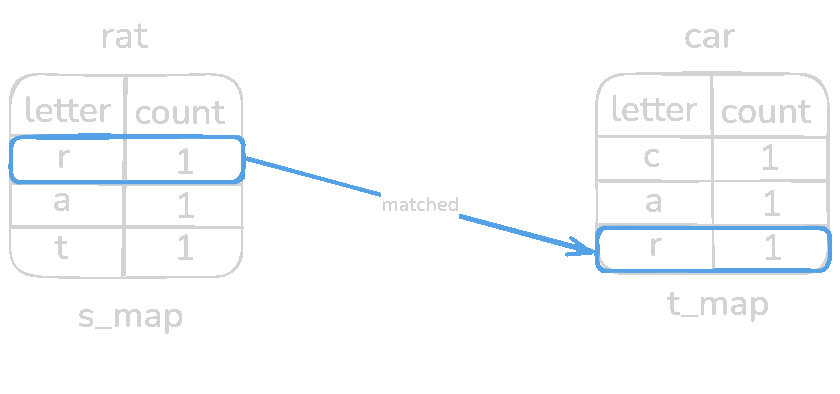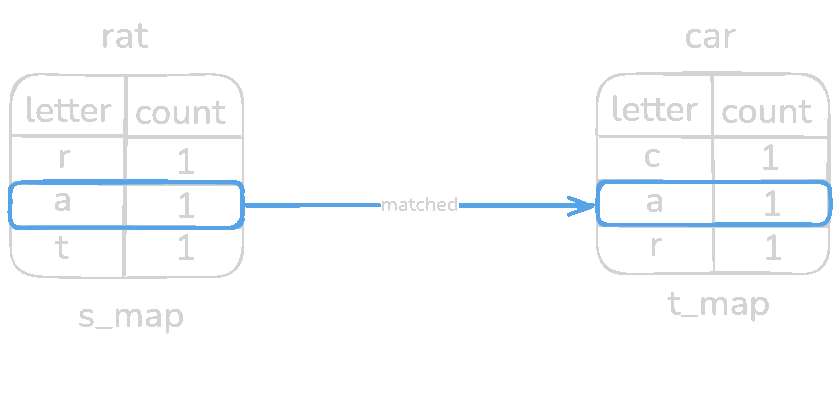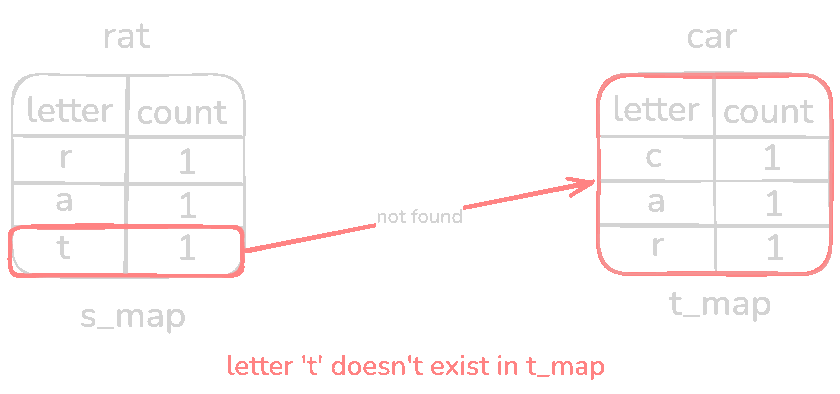
Every pair of s_map is equal to t_map meaning it's an anagram. Now test with a non-anagram input s = rat and t = car
Complete Code Snippet
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
s_map: dict[str, int] = {}
t_map: dict[str, int] = {}
# Populate hashmap {letter: count}
for i in range(len(s)):
s_map[s[i]] = s_map.get(s[i], 0) + 1
t_map[t[i]] = t_map.get(t[i], 0) + 1
# Match each letter and count from both of the maps
for letter in s_map.keys():
if letter not in t_map: # O(1) operation
return False
if s_map[letter] != t_map[letter]: # O(1) operation
return False
return True
Complexity Analysis
Time Complexity:
- HashMap lookup is almost instant, considering O(1) lookup time.
- Then we are iterating over two string and two hashmaps
- So the overall time complexity is
O(N), whereNis the number of letters in the strings
Space Complexity:
Since we have used an additional data-structure HashMap, so the overall space complexity would be O(N), where N is the number of pairs in the HashMap.
Thanks for Stopping by! Happy Leet coding
Connect with me on



