Two Sum

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

Acceptance Criteria:

• You may assume that each input would have exactly one solution
• You may not use the same element twice
• You can return the answer in any order.

Example 1:

Inputs: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:

Input: nums = [3,2,4], target = 6
Output: [1,2]
Explanation: Because nums[1] + nums[4] = 6, we return [1,2]

Example 3:

Input: nums = [3,3], target = 6
Output: [0,1]

Before going through this approach, check out the basic Two Sum (BruteForce) solution first

Intuition

We are aimed to optimized our previous solution, solving this problem in Linear time-complexity.
Let's take an example first
input = [7,11,15,2] and target = 9
expected output = [0, 3]
Like the previous solution, let's iterate from the 0th index.

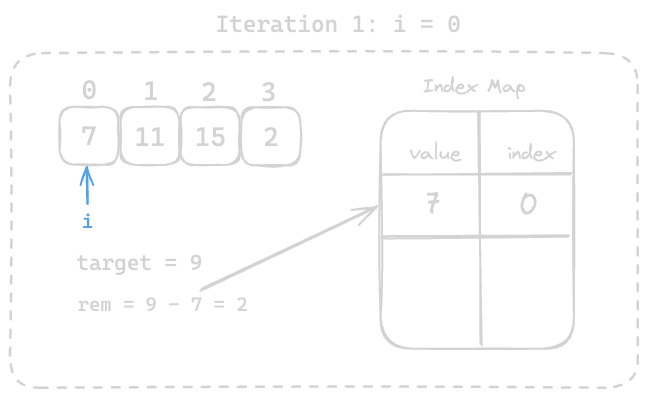
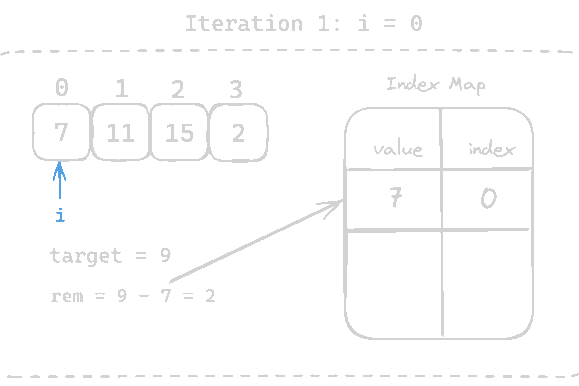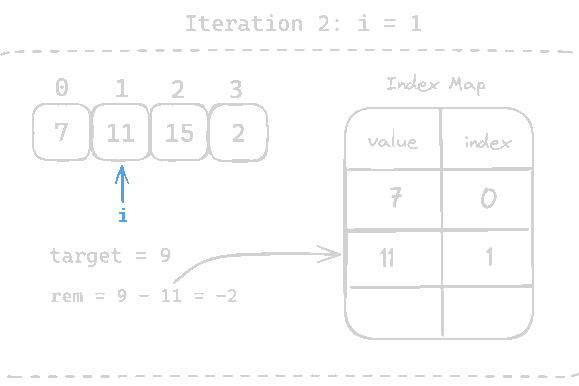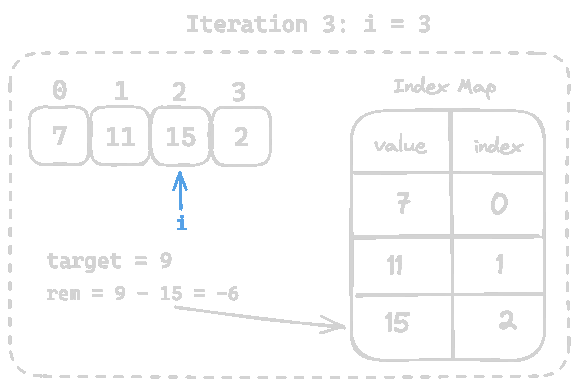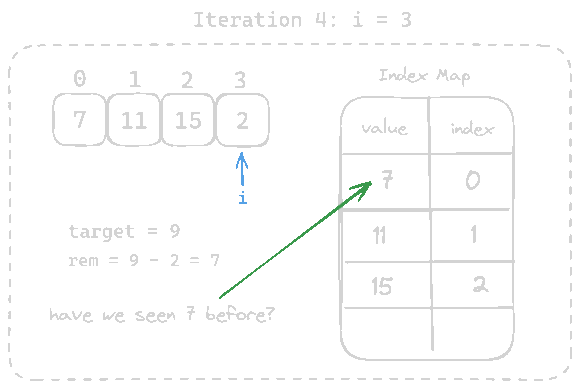
1. We subtract the target from the current value, e.g., 9 - 7 = 2.
2. We check if the result (2) already exists in the map. If it does, we have found our pair.
3. If it does not exist, we store the [value, index] pair in the map, indicating that we have visited 7 at index 0.
4. As we continue iterating, we may encounter 9 - 2 = 7. Since 7 is already in the map with index 0, we can return the indices like [index of 7, current index].

Here is the Flowchart for better understanding and visualization

Let's keep iterating through the list,

-2 doesn't exist in the map, so add current value 11 and it's index 1

-6 doesn't exist in the map, so add current value 15 and it's index 2

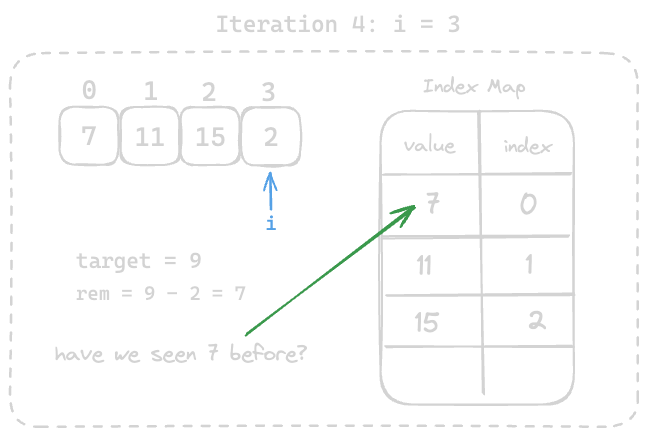
7 which already exists in the map and we can lookup the index of 7 from the map in O(1) time.
Finally, we can return the index of 7 and current index as an array.

Complete Code Snippet

class Solution:
	def twoSum(self, nums: List[int], target: int) -> List[int]:
		visited = {}
		for i in range(len(nums)):
			rem = target - nums[i]
			if rem in visited:
				return [visited[num[i]], i]
			visited[num[i]] = i
		return []

Complexity Analysis

Time Complexity

The given code uses a single pass approach with a hashmap (visited_map) for storing a pair of previously seen number and it's index. Let’s analyze its time complexity step by step:

• The for loop iterates over all n elements in nums, meaning the loop runs O(n) times.
• Each operation inside the loop (checking for rem in visited, inserting into the dictionary) takes O(1) time on average.
  Thus, the overall time complexity is O(n), making it significantly more efficient than the brute-force approach (O(n²)).

Space Complexity

The visited dictionary stores up to n key-value pairs, leading to a worst-case space complexity of O(n).

Final Complexity Summary

• Time Complexity: O(n) (Single pass with constant-time lookups)
• Space Complexity: O(n) (Hash table storage)

This optimized approach achieves better performance by trading extra space for faster lookups.

Thanks for Stopping by! Happy Leet coding

Connect with me on