Group Anagrams

Problem Statement

Given an array of strings strs, group the anagrams together. You can return the answer in any order.

Example:
Input: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
Output: [["bat"],["nat","tan"],["ate","eat","tea"]]
Explanation:

• There is no string in strs that can be rearranged to form "bat".
• The strings "nat" and "tan" are anagrams as they can be rearranged to form each other.
• The strings "ate", "eat", and "tea" are anagrams as they can be rearranged to form each other.

The given function signature looks like this

class Solution:
	def groupAnagrams(self, strs: List[str]) -> List[List[str]]:

Intuition

Let's take example 1, one way we can group it by constructing key-value pair like this. Where the key is the sorted value of the given strings and value is the group of anagrams.

{
	"aet": ["ate","eat","tea"],
	"ant": ["ant","nat","tan"],
	"abt": ["bat"]
}

Why it works? Because, the sorted value is identical for anagram strings. Checkout Valid Anagram to get more knowledge around this.

Sorting Solution

All we need to iterate through the strs = ["eat", "tea", "tan", "ate", "nat", "bat"]. Then make the key and group the anagrams togather. Let's visualize the process

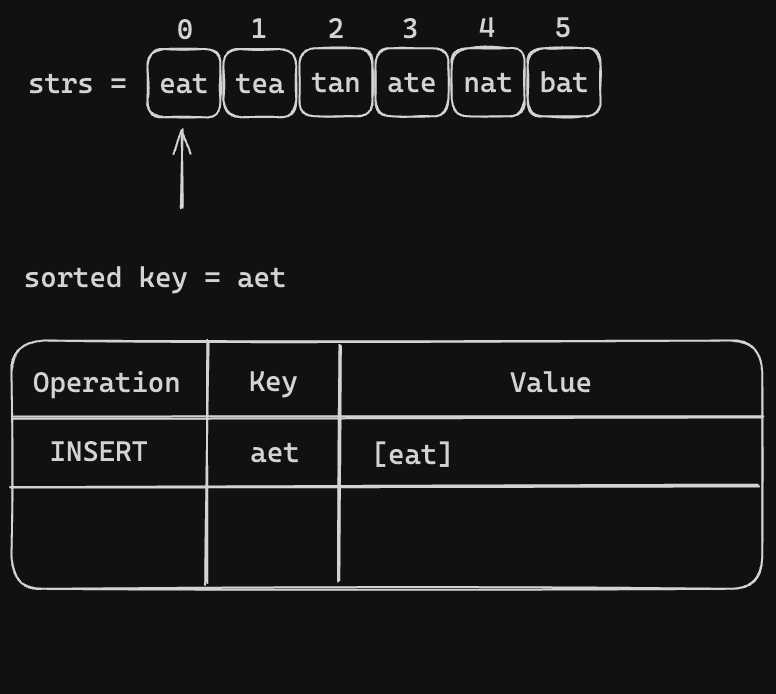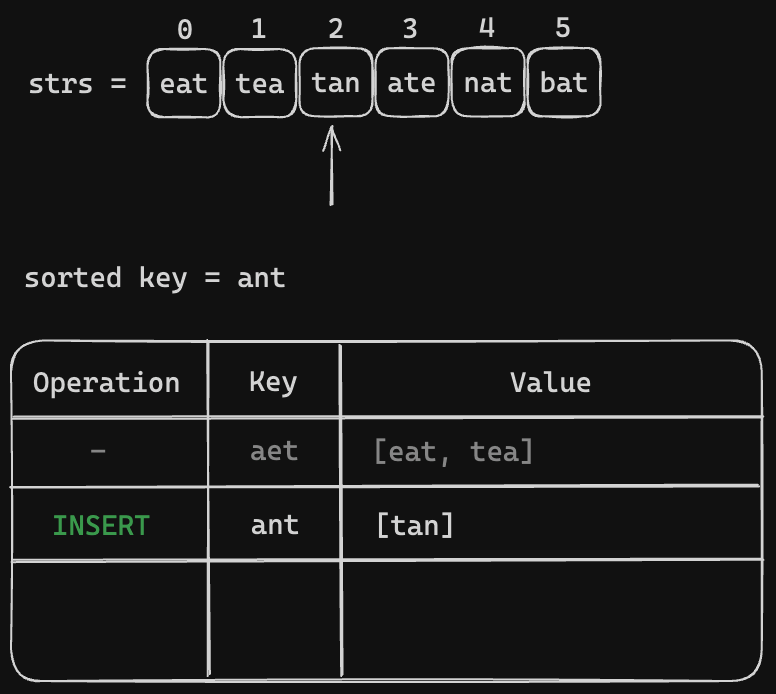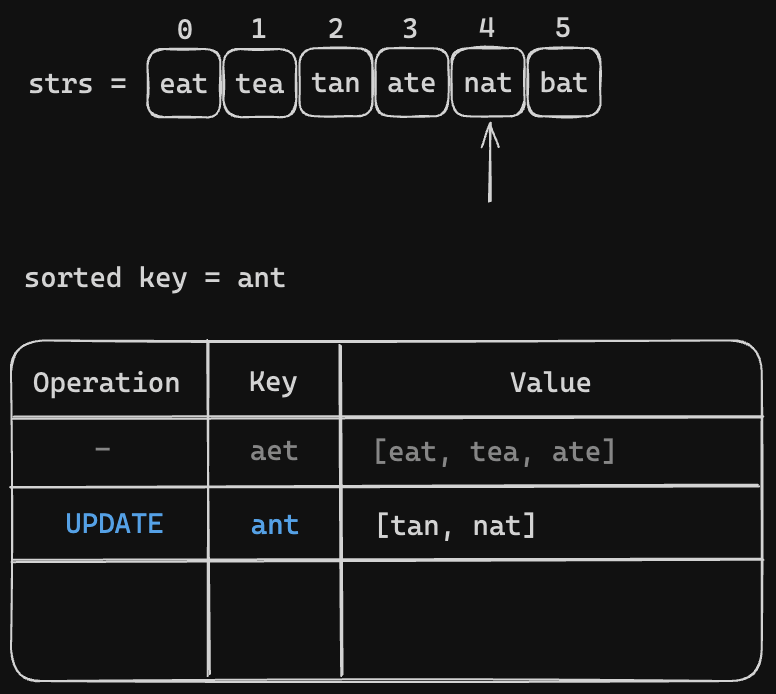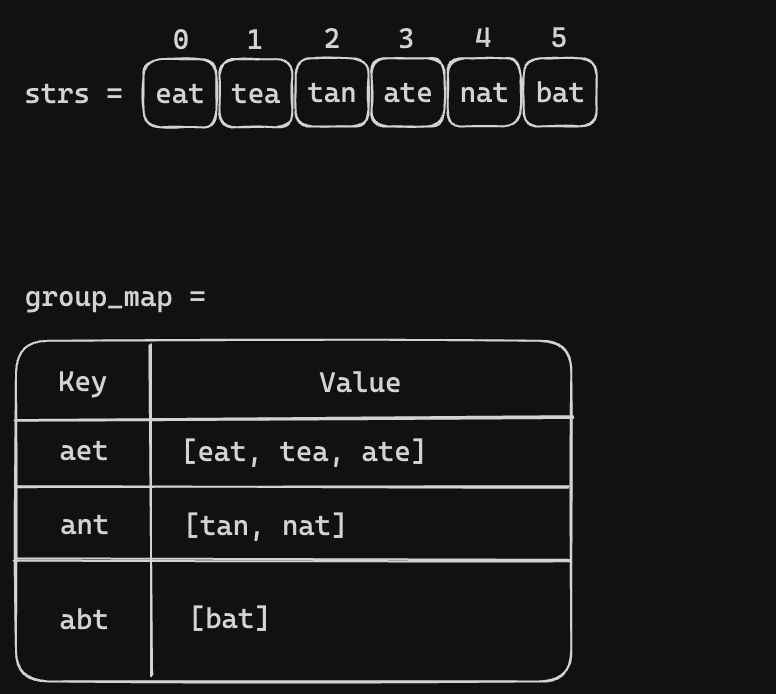
Code Snippet (Sorted Key)

class Solution:
	def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
		# handle edge case
		if not strs: return []
		
		group_map: dict[str, list] = {}
		# Looping takes O(n) time
		for s in strs:
			key = self.get_key(s) # O(nLogn)
			# when the key is new
			if key not in group_map:
				group_map[key] = [s]
			else:
				# otherwise append string in the group list
				group: list = group_map[key]
				group.append(s)
				group_map[key] = group
		
		# now return the list of groups as a list of list
		return list(group_map.values())

	# helper function to make the key
	def get_key(self, s: str) -> str:
		# need to optimize this function
		return "".join(sorted(s.lower()))  # merge sort taken O(nLogn) time 

Complexity Analysis

Time Complexity:

• The for loop is taking O(n) time where n is the number of strings in the given list strs
• But the helper function get_key uses sorting to make the key which is taking O(nlogk) time. Where n is the number of strings in the strs list and k is the largest string among strs list items.
• So the overall time complexity is O(nLogk)
  Space Complexity:
• Since we are using additional HashMap data-structure, the space complexity is O(n), where n is the number of strings in the given list strs

More Optimal Approach

We have identified that sorting is taking O(nLogk) time. Our objective is to eliminate the need for sorting and implement an alternative approach that computes the key in linear time. The primary focus now is to optimize the get_key function, reducing its complexity from O(nlogk) to O(k). Let's explore this in depth.

Optimize Get Key function

Using HashMap

One way to generate a key is by concatenating the letters with their frequencies for a given word.

The first idea that comes to mind is using a HashMap to store each letter along with its frequency—just as we did in Valid Anagram. We can then utilize these letter : count pairs to construct the key efficiently.

Let's start by implementing the get_key function using a HashMap.

def get_key(self, word: str) -> str:
	# we know that eat and tea are anagrams
	# and this funciton should return same key for eat and tea
	count_map: dict[str, int] = {} 
	for ch in word:
		count_map[ch] = count_map.get(ch, 0) + 1
	key_segments = []
	for letter, count in count_map.items():
		key_segments.append(letter)
		key_segments.append(count)
	retutn "".join(key_segments)

Let's visualize and comapre the output of the function for eat and tea

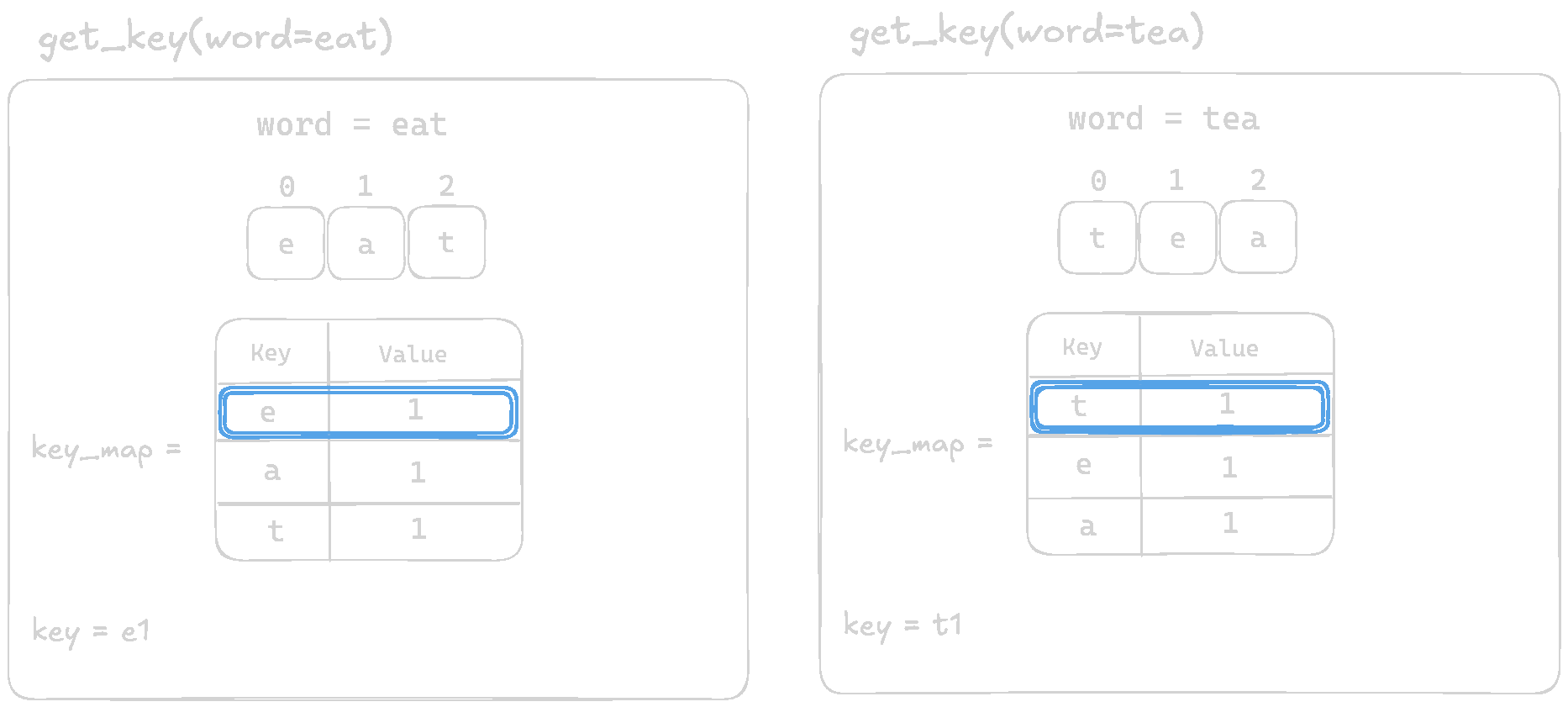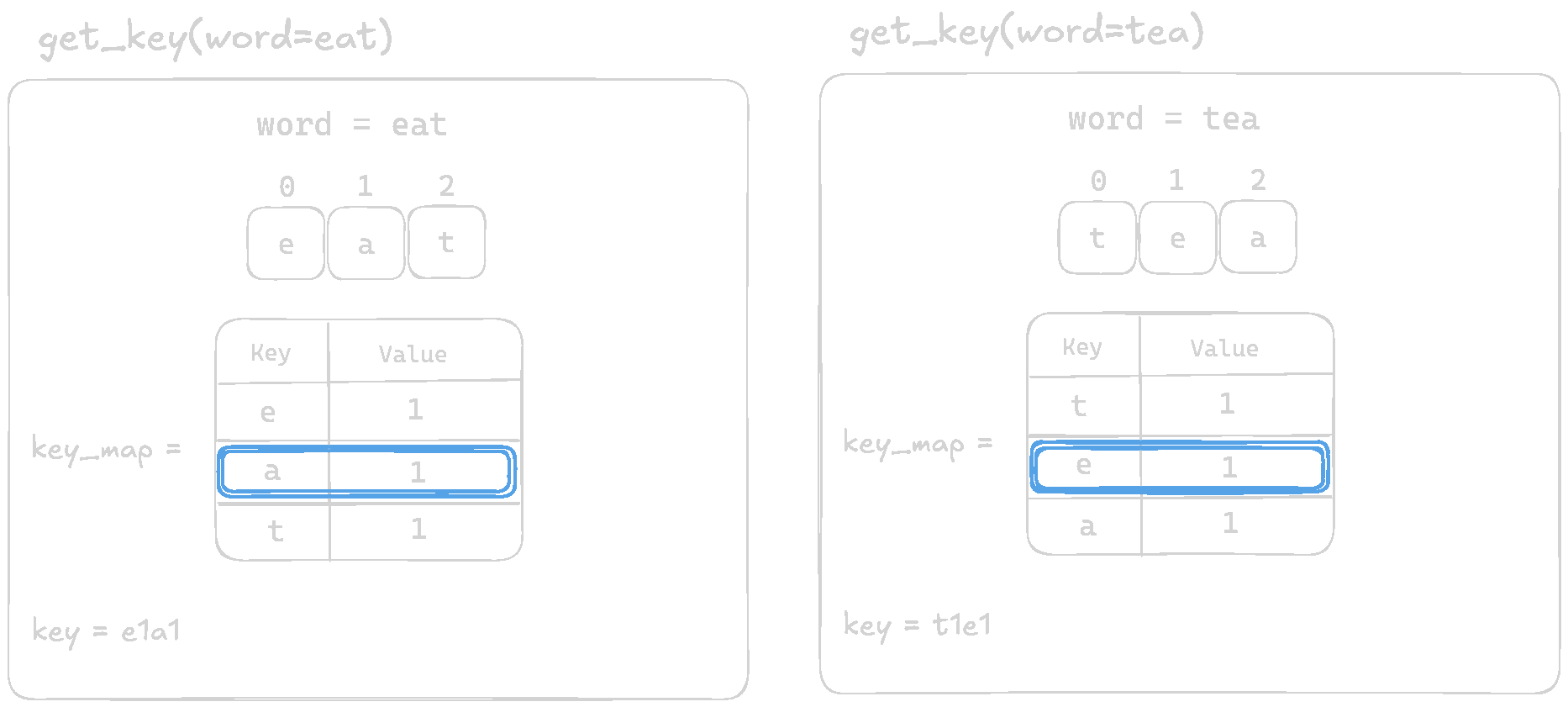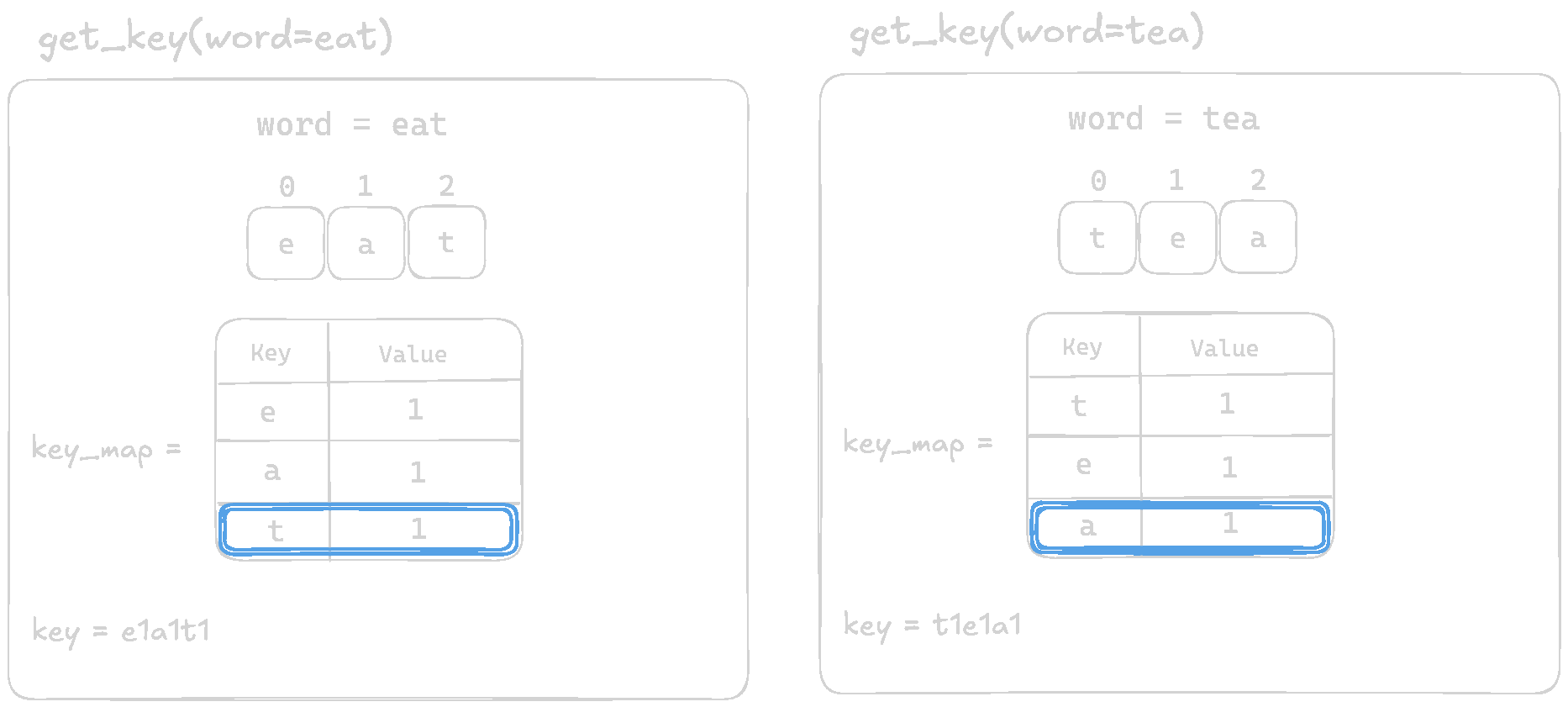
The function is returning different keys for anagrams like eat and tea when they should produce the same key. For eat, we get e1a1t1, while for tea, we get t1e1a1. Since the order of letters is not consistent, our solution breaks when grouping words.

{
	"e1a1t1": ["eat"],
	"t1e1a1": ["tea"]
	...
}

Instead of relying on the unordered nature of the HashMap, we need a way to ensure a consistent order when constructing the key. New challenge, how can we create an ordered key which will be always same for the anagrams?

Using Frequency Array

The idea is to map the 26 English letters (a to z) to an array of 26 indices (0 to 25).

We start by initializing an array with all zeros, ensuring that each letter has a fixed position for counting occurrences. This guarantees a consistent order when constructing the key.

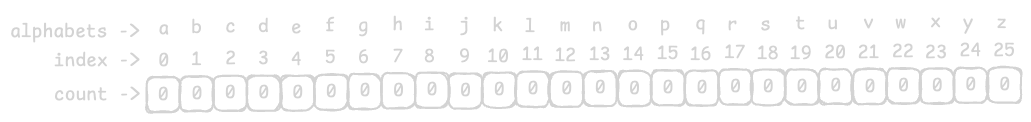
def get_key(self, word: str) -> str:
	freq_list: list = [0] * 26
	ascii_offset: int = ord('a')  # 97 is the ascii of `a` 

ASCII to Array Index Mapping

We will use the ASCII values of letters to map them to the correct indices in our array.
For example, to map 'b' to index 1, we will subtract the ASCII value of 'a' from the ASCII value of 'b'

Populate Frequency and Make key

Now let's populate the count of each letters in the given word.

def get_key(self, word: str) -> str:
	freq_list: list = [0] * 26
	ascii_offset: int = ord('a')  # 97 is the ascii of `a` 
	
	# Populate frequency of the each letters
	for ch in word:
		index = ord(ch) - ascii_offset
		freq_list[index]+= 1

Again, let's compare between eat and tea

After populating the frequency list, it will look like this

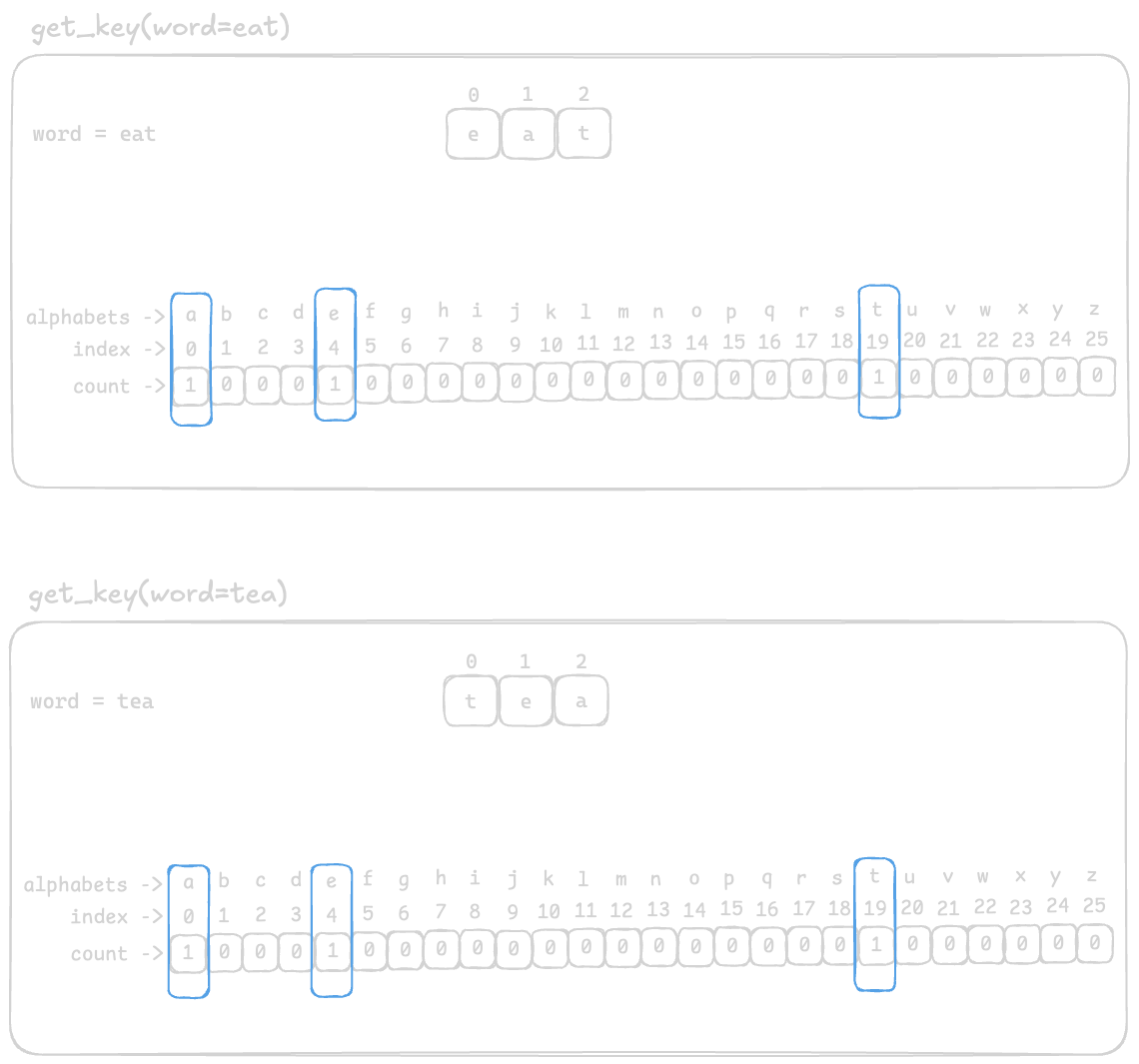
Now, we just need to construct the key from the frequency list.
To keep the key short, we will only include indices where the count is greater than 0.

def get_key(self, word: str) -> str:
	freq_list: list = [0] * 26
	ascii_offset: int = ord('a')  # 97 is the ascii of `a` 
	
	# Populate frequency of the each letters
	for ch in word:
		index = ord(ch) - ascii_offset
		freq_list[index]+= 1
	
	# Make Key from the frequency list
	key_segments = []
	for i in range(len(freq_list)):
		count = freq_list[i]
		if count > 0:
			# convert current index back to a letter
			letter = chr(i + ascii_offset)
			key_segments.append(letter)
			key_segments.append(count)
	return "".join(key_segments)

Let's visualize the counting process,

Great! Now, the get_key function generates identical keys for anagrams like "eat" and "tea", ensuring they are grouped correctly.

Additionally, we have optimized the time complexity to O(k), where k is the length of the longest string in the given array strs. This is a significant improvement over the previous O(n log k) sorting approach!

Since the frequency array has a fixed size of 26 (for English letters), the complexity O(26) simplifies to O(1).

After plugin this get_key function with our main solution, we will get a group like

{
	"a1e1t1": ["ate","eat","tea"],
	"a1n1t1": ["ant","nat","tan"],
	"a1b1t1": ["bat"]
}

If you still have confusion why need the counts concatenated with the letters, because a letter can appear multiple times e.g. {"b1e2r1t2": ["better", "rebter"]}.

Complete Code Snippet (Optimized)

class Solution:
	def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
		# handle edge case
		if not strs: return []
		
		group_map: dict[str, list] = {}
		# Looping takes O(n) time
		for s in strs:
			key = self.get_key(s) # O(k)
			# when the key is new
			if key not in group_map:
				group_map[key] = [s]
			else:
				# otherwise append string in the group list
				group: list = group_map[key]
				group.append(s)
				group_map[key] = group
		
		# now return the list of groups as a list of list
		return list(group_map.values())

	# helper function to make the key
	def get_key(self, s: str) -> str:
		freq_list: list = [0] * 26
		ascii_offset: int = ord('a')  # 97 is the ascii of `a` 
		
		# Populate frequency of the each letters
		for ch in word:
			index = ord(ch) - ascii_offset
			freq_list[index]+= 1
		
		# Make Key from the frequency list
		key_segments = []
		for i in range(len(freq_list)):
			count = freq_list[i]
			if count > 0:
				# convert current index back to a letter
				letter = chr(i + ascii_offset)
				key_segments.append(letter)
				key_segments.append(count)
		return "".join(key_segments)

Final Output:

[
	["ate","eat","tea"],
	["ant","nat","tan"],
	["bat"]
]

Complexity Analysis

Time Complexity Analysis:

• The for loop takes O(n) where n is the number of strings in the strs string array
• Inside the for loop, get_key function takes O(k) time where k is the longest string in the string array strs
• So the overall time complexity is O(n * k) which is better than O(nlogn)
  Space Complexity:
• The frequency list freq_list is always of size 26, which is a constant (O(26) = O(1)).
• The dictionary group_map stores n keys (in the worst case, each word forms its own group).
• So the overall space complexity is O(n)

Thanks for Stopping by! Happy Leet coding

Connect with me on